I. Optimiser les réseaux

Comme nous avons pu le comprendre, la priorité pour qu’un village puisse accéder de façon stable à l’eau et à l’électricité, est d’optimiser au mieux son réseau de distribution pour éviter toute perte inutile et précieuse dans une région isolée.

Pour cela nous avons créé un algorithme permettant de simuler la consommation d’un village pendant une période de 31 jours. Chaque village est modélisé de telle sorte :

Les maisons sont reliées entre elles avec un câble (chaque câble va dans les deux sens). La position et le nombre de maisons est complètement aléatoire.

A. Structure

La structure prend en compte tous les éléments physiques du réseau qui peuvent varier, tels que l’emplacement de la production électrique par exemple.

Dans notre cas, la source d’énergie sera les panneaux solaires car comme nous l’avons vu plus tôt, c’est la plus adaptée à de telles zones isolées.

Nous avons également besoin de calculer les pertes totales d’un tel réseau. La première partie de notre expérience consiste à tester lequel des types de courant est le plus “optimisé”: continu ou alternatif.

Après avoir fait plusieurs tests, nous sommes arrivés à la conclusion que le courant continu est plus efficace et performant à petite échelle (les villages que nous étudions sont relativement petits).

Voici les résultats que nous avons pu observer:

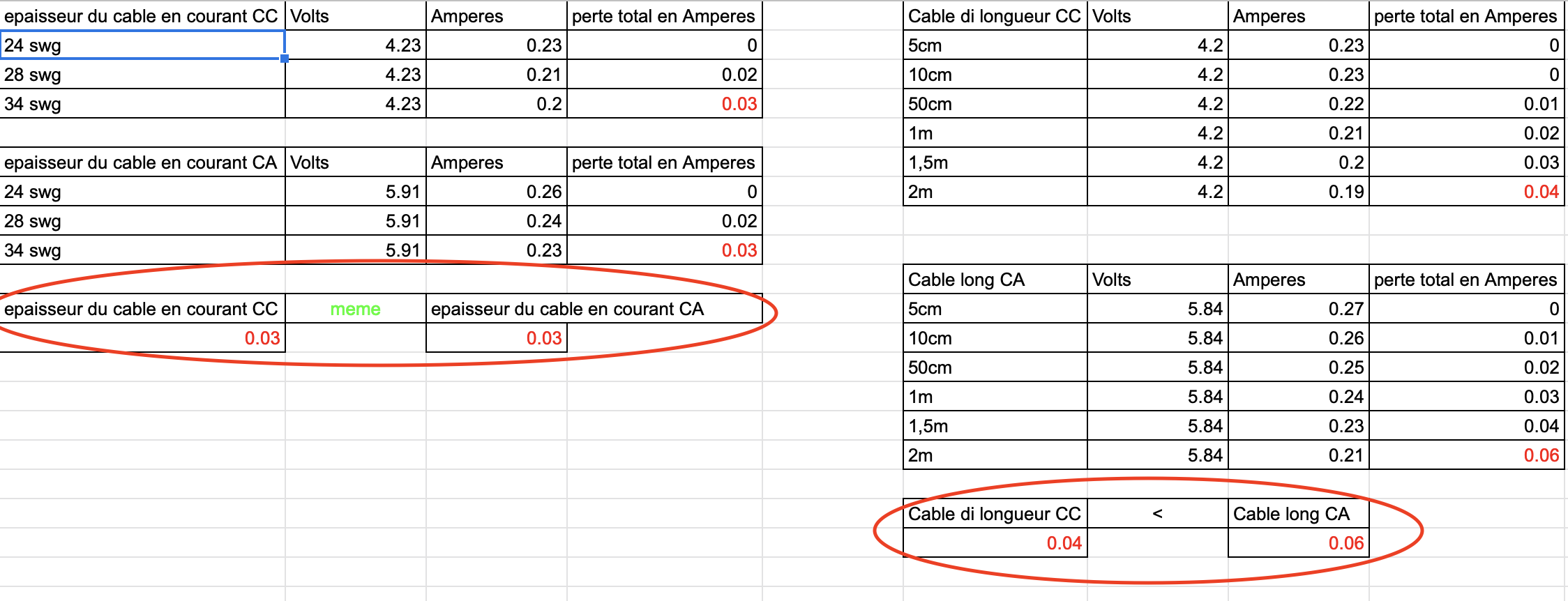
La perte est plus importante en utilisant le courant continu que alternatif.

Puis, à l’aide d’un algorithme que nous avons développé et dans lequel nous attribuons certaines caractéristiques (consommation, taille de câbles, type de production (ferme solaire vs panneau individuel), etc…) nous simulons la consommation électrique de plusieurs villages. Enfin, nous faisons tourner les simulations afin de les classer par pertes et par bilan total (correspond à la production supplémentaire du village par rapport à sa consommation).

B. Ressources

Pour rendre fonctionnelle cette simulation dans une zone isolée, nous avons évalué les ressources nécessaires à sa construction. Il est d’abord nécessaire d’avoir autant de panneaux solaires qu’il y a de maisons. Pour réduire de façon considérable les pertes, chaque panneau sera directement fixé sur le toit d’une maison. Il peut également y en avoir quelques uns en  plus si le village possède une école ou un plus grand bâtiment.

Il faudra également relier électriquement chaque maison aux deux maisons les plus proches afin de mettre en commun leurs ressources électriques. C’est à dire que si une maison consomme plus que les autres, elle pourra utiliser l’énergie produite en excès par les panneaux solaires voisins et inversement. C’est donc un réseau intelligent qui calcule en temps réel la consommation de chaque maison pour diminuer les pertes d’énergie. Il faut savoir que toute énergie produite par un panneau solaire est perdue si elle n’est pas stockée ou utilisée tout de suite. De plus, les panneaux solaires ne fonctionnant pas la nuit, nous pensons que la meilleure solution est l’installation d’une petite batterie par maison permettant de stocker suffisamment d’énergie pour une nuit.

De plus, les câbles ne sont pas une ressource à oublier, leurs matériaux vont grandement faire varier les pertes. Afin de calculer les pertes, il nous faut d’abord calculer la résistance du câble avec la loi de la conductivité:$$R=\rho \frac{l}{S}$$

Aussi connu sous le nom de la loi de Pouillet

Puis, si l’on connait l’intensité du courant, on peut alors en déduire les pertes grâce à l’effet de Joule.$$P=RI^2$$

D’où la relation finale: $$P=\rho \frac{l\times{I^2}}{S}$$

Définitions

P (W): Puissance perdue en chaleur
ρ (Ω⋅m): Résistivité du métal utilisé
l (m): Longueur du cable
I (A): Intensité du courant
S (m²): aire de la section du cable, c'est à dire le carré de son diamètre (si le fil a une section circulaire)

C. Résultats

Après avoir testé plusieurs longueurs de câble, dans plusieurs conditions, nous avons conclu que le courant continu a tendance à perdre moins d’énergie pour un petit réseau. De plus, nous avons pu observer et implementer la relation finale $$P=\rho \frac{l\times{I^2}}{S}$$Nous décidons donc d’utiliser le courant continu dans notre algorithme.

Après avoir fait tourner la simulation à l’aide d’un algorithme sur l’équivalent d’une période de 31 jours, nous avons constatés les résultats suivants:

See the Pen Chart - TPE by Arthur Guiot (@arguiot) on CodePen.

Definitions

P: Est-ce que chaque maison produit ou non sa propre électricité?
F: Facteur de production par rapport à la consommation
A: Ampérage (sert à calculer la perte)
Ro: Résistance du cable utilisé (par rapport a la matière)

Les résultats montrent que la production d’électricité en utilisant un système de production individuelle (un panneau solaire par maison) est bien plus rentable est performant qu’un réseau utilisant une production centralisée.

II. Apporter les ressources

Afin de développer et construire un réseau intelligent, il est crucial d’avoir le matériel humain et physique nécessaire. Or, dans une zone isolée, c’est un tout autre problème que dans un endroit conventionnel.

A. Infrastructure

Le premier problème rencontré est la construction de l’infrastructure nécessaire pour créer de tels réseaux. Plusieurs solutions s’offrent à nous. La première serait de construire un réseau basé à l’extérieur mais comme notre expérience l’a démontré, ce n’est pas la bonne solution.

L’autre idée serait de pré construire des “bouts” ou des parties du réseau et de les assembler sur place, tel un meuble de la fameuse marque suédoise. Ainsi, il est bien plus simple à produire, et cette solution offre la possibilité de la production en masse, produire des parties à l’extérieur de la zone semble donc être la solution idéale pour répondre au problème de production.

B. Humain

Le second problème, c’est le nombre d’ouvriers nécessaires pour assembler le réseau. Les habitants ne pourront pas tous aider à l’assemblage car cela requiert un certain niveau d’expertise.

Afin de créer un tel réseau pour un village de 12 maisons, on peut considérer que 5 ouvriers est un nombre acceptable. Le salaire moyen en Afrique étant de 156 $ / mois on peut estimer à 768$ le coût humain mensuel pour cette petite équipe. Le petit nombre de cette équipe facilite le recrutement de personnel et ne devrait pas poser de gros problèmes.

Le coût technologique devient donc la seul contrainte. Trouver des employés dans des pays où le taux d’emploi est plus bas que la moyenne est relativement simple, à condition d’un salaire correct.

C. Technologie

En effet, c’est cette dépense qui sera la plus élevée pour créer un réseau intelligent dans un village car les coûts technologiques des panneaux solaires ou des batteries par exemple sont élevés et ne peuvent pas vraiment être diminués. Il est très dur de diminuer ce coût car les technologies actuelles (même les plus avancées) utilisent des matériaux rares et dur à extraire. Le seul paramètre que l’on peut baisser, c’est le coût d’assemblage, qui est principalement lié à la production de masse. Or, si les gouvernements ou les banques acceptaient de financer la production massive de panneaux solaires, le coût pourrait drastiquement baisser et le projet de connecter les zones isolées pourrait voir le jour.